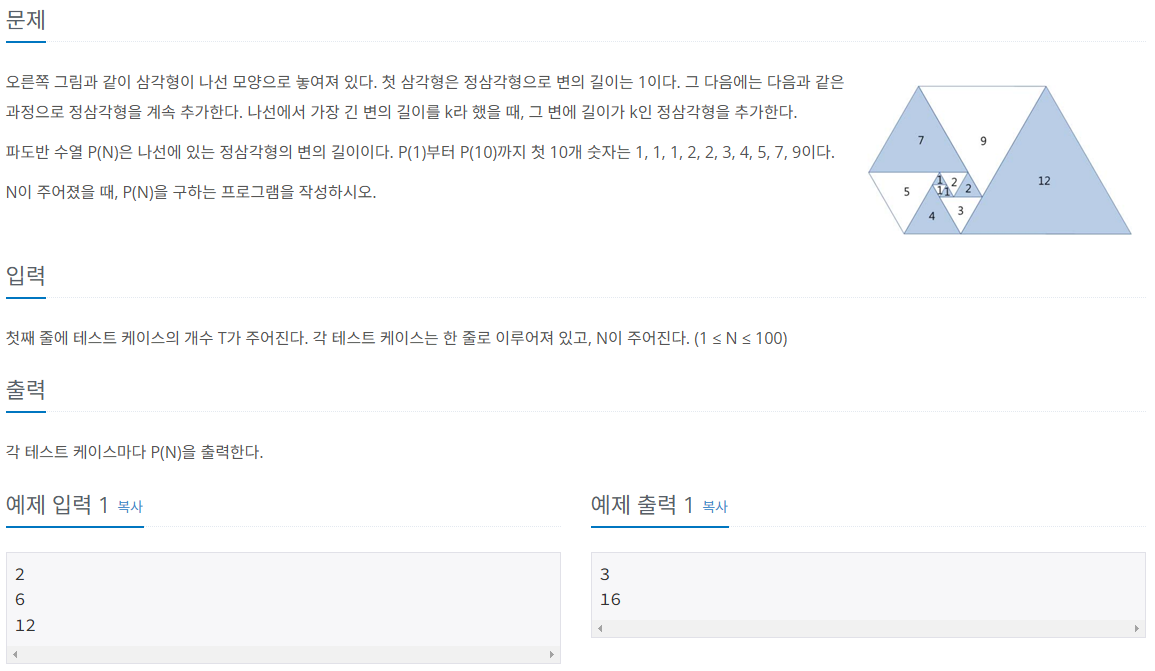
파도반 수열이라 하니 비슷한 피포나치 수열이 생각난다. 억지
피보나치수열에는 패턴이 존재하는데, 파도반 수열 문제에 나열된 숫자들도 어떤 패턴을 가지고 있을 것 같다.
피보나치 수열
N = 10 조건을 가지는 피보나치수열을 구한다면 1 + 1 + 2 + 3 + 5 + 8 + 13 + 22 + 35 + 55이다.
F(1) = F(2) = 1의 초기값을 가지며 점화식으로 F(n) = F(n-1) + F(n-2)가 된다.
파도반 수열
먼저 변의 길이는 생각하지 말고(?) 규칙을 찾기 위한 삼각형을 그려보자.
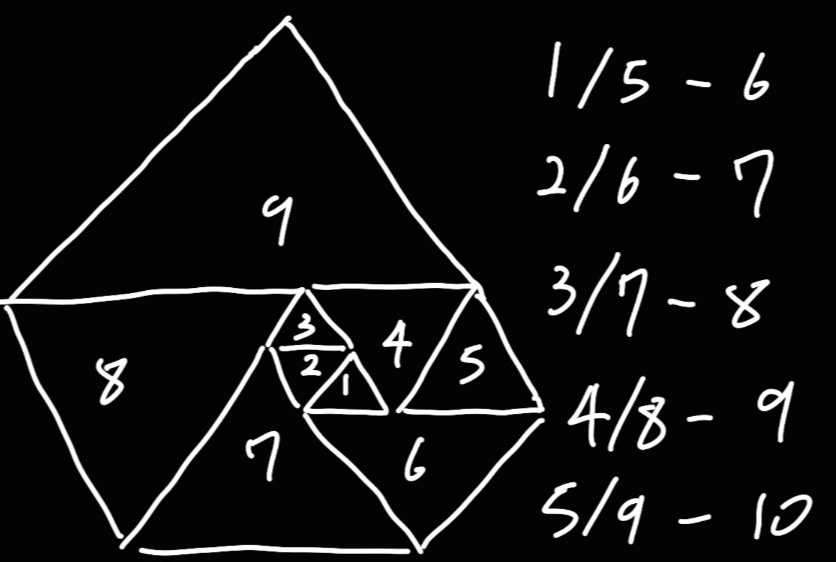
여러 방식으로 그림을 그려봤지만 이 그림에서 규칙을 찾게 되었다.
문제의 1, 1, 1, 2, 2, 3, 4, 5, 7, 9 수열에서 보면 4번 삼각형을 그렸을 때 변의 길이가 늘어나기 시작하고,
6번 삼각형을 그릴 때부터 패턴을 가지는 것을 볼 수 있다.
6번 삼각형이 만들어지기 위해 1번과 5번,
7번 삼각형이 만들어지기 위해 2번과 6번...
이 규칙을 공식화해 보면 P(6) = P(6 - 1) + P(6 - 5) / P(7) = P(7 - 1) + P(7 - 5)
즉, F(n) = F(n-1) + F(n-5)가 된다.
하지만 위 공식을 사용하려면 4번 삼각형까지 초기값을 가져야 한다.
문제에서 초기값을 가질 수 있는 삼각형은 3번 삼각형까지다.
특정 삼각형 변의 길이를 구하기 위해 평행선을 긋고 평행사변형을 만들어보며 공식을 구하는 방법도 있다.
위 방법을 사용했을 때 F(n) = F(n-2) + F(n-3) 공식이 성립된다.
내 그림은 너무 난잡해서 올리질 못하겠다..
구현
import java.io.*;
public class Main {
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringBuilder sb = new StringBuilder();
int T = Integer.parseInt(br.readLine());
for (int i = 0; i < T; i++) {
int N = Integer.parseInt(br.readLine());
long result = padovan(N);
sb.append(result).append("\n");
}
System.out.println(sb);
br.close();
}
private static long padovan(int N) {
if (N < 4) {
return 1;
}
long[] arr = new long[N + 1];
// 3번 삼각형까지 초기값 설정
arr[1] = arr[2] = arr[3] = 1;
for (int i = 4; i <= N; i++) {
arr[i] = arr[i-2] + arr[i-3];
}
return arr[N];
}
}백준 9461번 - 파도반 수열
'코딩테스트 > 99클럽 4기' 카테고리의 다른 글
| 99클럽 코테 스터디 31일차 TIL (0) | 2024.11.27 |
|---|---|
| 99클럽 코테 스터디 30일차 TIL (1) | 2024.11.26 |
| 99클럽 코테 스터디 28일차 TIL (0) | 2024.11.24 |
| 99클럽 코테 스터디 27일차 TIL (0) | 2024.11.23 |
| 99클럽 코테 스터디 26일차 TIL (0) | 2024.11.22 |